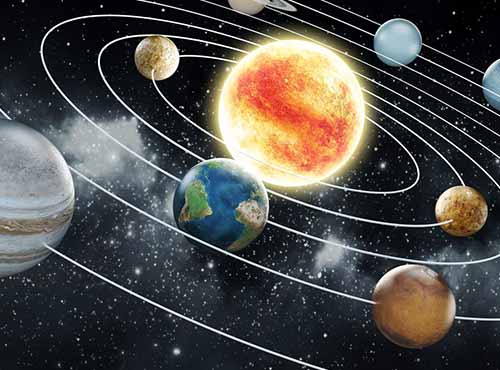
តើអ្នកវិទ្យាសាស្ត្រអាចគណនាចម្ងាយវត្ថុរាប់ពាន់លានគីឡូម៉ែត្រនៅលើលំហពីផែនដីយ៉ាងដូចម្ដេច ?
អ្នកដែលបានសិក្សាកន្លងមកធ្លាប់តែដឹងថា ព្រះអាទិត្យមានចម្ងាយ១៤៩,៦០០,០០០គីឡូម៉ែត្រពីភពផែនដី។ ប៉ុន្តែតើអ្នកធ្លាប់ឆ្ងល់ដែរទេថា តើអ្នកវិទ្យាសាស្ត្របានតួលេខយ៉ាងច្រើនសម្បើមបែបនេះបានដោយរបៀបណា ? តើពួកគេត្រូវបញ្ជូនមនុស្សតាមយានអវកាសទៅកាន់ព្រះអាទិត្យ ដើម្បីគណនាចម្ងាយនេះឬ ? អ្នកដឹងរួចមកហើយថា ផែនដីវិលជុំវិញខ្លួនឯងនិងព្រះអាទិត្យ ហើយ១ជុំដែលផែនដីវិលបានជុំវិញព្រះអាទិត្យស្មើនឹង១ឆ្នាំនៅលើភពផែនដីមែនទេ ? នេះហើយគឺជាដើមទុននៃគន្លឹះដ៏មុតស្រួចមួយ ដែលអាចនាំអ្នកវិទ្យាសាស្ត្រឲ្យគណនាពីចម្ងាយរបស់ផ្កាយឬភពផ្សេងៗដែលនៅឆ្ងាយរាប់ពាន់លានគីឡូម៉ែត្របាន។
ដើម្បីឲ្យការស្វែងយល់ពីការអនុវត្តជាក់ស្ដែងពីរបៀបនៃការគណនាចម្ងាយវត្ថុនៅលើលំហរបស់អ្នកវិទ្យាសាស្ត្របានងាយស្រួល យើងគួរស្វែងយល់ពីឧទាហរណ៍ដ៏សាមញ្ញនៅក្នុងជីវិតប្រចាំថ្ងៃជាមុនសិន។ អ្នកអាចលាតដៃរបស់អ្នកទៅមុខ ហើយលើកមេដៃមួយឡើងដោយរក្សាទីតាំងវាមិនឲ្យផ្លាស់ប្ដូរ។ បន្ទាប់មកបិទភ្នែកខាងឆ្វេងតែទុកភ្នែកខាងស្ដាំនៅបើកដដែល ហើយសង្កេតទីតាំងមេដៃរបស់អ្នក។ ម្ដងនេះសាកបិទភ្នែកខាងស្ដាំហើយទុកភ្នែកខាងឆ្វេងនៅបើកវិញ ហើយសង្កេតទីតាំងមេដៃរបស់អ្នកម្ដងទៀត។ តើអ្នកមានសង្កេតថា មេដៃរបស់អ្នកប្ដូរពីទីតាំងមួយទៅទីតាំងមួយផ្សេងទៀតទេ ?
វាជាចលនាភ្នែករបស់អ្នកដែលម្ដងបិទម្ដងបើក ដែលធ្វើឲ្យអ្នកមានអារម្មណ៍ថាមេដៃរបស់អ្នកផ្លាស់ប្ដូរទីតាំង ទាំងដែលវារក្សាទីតាំងនៅនឹងមួយកន្លែង។ ដោយដឹងពីចម្ងាយពីភ្នែកម្ខាងរបស់អ្នកទៅភ្នែកម្ខាងទៀត ហើយដឹងពីចម្ងាយពីទីតាំងមួយទៅទីតាំងមួយទៀតដែលមេដៃផ្លាស់ប្ដូរនៅពេលបិទបើកភ្នែកម្ខាង ដែលបង្កើតជាមុំ នោះគេនឹងអាចគណនាដឹងពីចម្ងាយពីភ្នែករបស់អ្នកទៅកាន់មេដៃបាន ដែលគេហៅវិធីសាស្ត្រគណនានេះថា "Trigonometric Parallex"។
[caption id="attachment_43161" align="aligncenter" width="600"]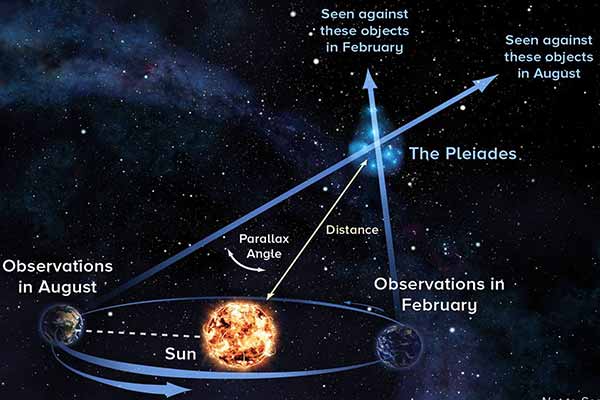
www.space.com[/caption]
Trigonometric Parallex មានពាក្យ Trigonometric ដែលសំដៅទៅលើត្រីកោណមាត្រ និងពាក្យ Parallex ដែលសំដៅទៅលើចំណុចផ្លាស់ប្ដូររបស់ផ្កាយណាមួយដែលគេចង់វាស់ចម្ងាយរបស់វា ធៀបទៅនឹងចំណុចនឹងថ្កល់របស់ផ្កាយដែលមានទីតាំងឆ្ងាយ នៅពេលផែនដីធ្វើចលនាវិលជុំវិញព្រះអាទិត្យដែលជាចំណុចកណ្ដាលរបស់ប្រព័ន្ធព្រះអាទិត្យបានរយៈពេលកន្លះឆ្នាំ។
១ឆ្នាំផែនដីវិលជុំវិញព្រះអាទិត្យបាន១ជុំ ដូច្នេះរយៈពេលកន្លះឆ្នាំផែនដីវិលបានកន្លះជុំ។ ដោយសារចលនារង្វិលជុំរបស់ផែនដីជុំវិញព្រះអាទិត្យមានរាងជាអេលីប នោះផែនដីវិលជុំវិញព្រះអាទិត្យបាន១ជុំ ១ជុំឬ១រង្វង់នេះបង្កើតបានអង្កត់ផ្ចិត។ យើងដឹងថាចម្ងាយពីផែនដីទៅព្រះអាទិត្យមាន១៤៩,៦០០,០០០គីឡូម៉ែត្រ ដែលស្មើនឹងពាក់កណ្ដាលអង្កត់ផ្ចិតរបស់១ជុំឬ១រង្វង់ដែលផែនដីធ្វើចលនាវិលជុំវិញព្រះអាទិត្យបាន១ឆ្នាំ។ ចម្ងាយដែលផែនដីវិលជុំវិញព្រះអាទិត្យបានកន្លះឆ្នាំ ឬជាចម្ងាយពីផែនដីទៅព្រះអាទិត្យតែម្ដងត្រូវបានអ្នកវិទ្យាសាស្ត្រកំណត់យកជាមាត្រដ្ឋានសម្រាប់គណនារកចម្ងាយផ្កាយផ្សេងៗទៀតផងដែរ ដែលគេសរសេរថា ១AU = ៩៣ពាន់លានម៉ៃល៍ (១៤៩,៦០០,០០០គីឡូម៉ែត្រ)។
ដូច្នេះគឺផែនដីជាអ្នកមានចលនារង្វិល ហេតុនេះនៅពេលសម្លឹងមើលផ្កាយ ឧទាហរណ៍ថាក្នុងខែមករា លុះដល់ពេល៦ខែក្រោយមក ឬបានពាក់កណ្ដាលជុំដែលផែនដីវិលជុំវិញព្រះអាទិត្យ នោះអ្នកនឹងសង្កេតឃើញថាផ្កាយដដែលនេះនឹងផ្លាស់ទីទៅម្ខាងទៀត ដែលមានទិសផ្ទុយគ្នានឹងទិសកាលពីអ្នកមើល៦ខែមុន ដូចដែលអ្នកបិទបើកភ្នែកម្ខាងដូច្នោះ។ ចម្ងាយពីផែនដីទៅផ្កាយណាមួយមុននឹងក្រោយ៦ខែ វានឹងជួបគ្នាត្រង់ចំណុចផ្គួបណាមួយ ហើយចម្ងាយពីចំណុចផ្គួបមកកាន់ផែនដីនេះហើយគឺជាចម្ងាយពិតប្រាកដរបស់ផ្កាយនេះពីផែនដី ដែលតាងដែលD។ តើយើងអាចគណនាដូចម្ដេចបាន នៅពេលយើងទទួលបានត្រីកោណនេះហើយ ? ចម្ងាយD នឹងបែងចែកត្រីកោណដ៏ធំមួយនេះជាត្រីកោណកែងពីរ។ អ្នកដឹងហើយថាកំពូលមុំរបស់ត្រីកោណកែងមានរង្វាស់មុំ៩០ដឺក្រេ។
[caption id="attachment_43160" align="aligncenter" width="600"]
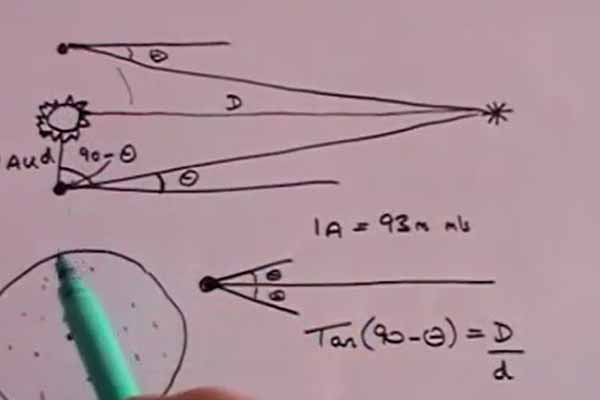DrPhysicsA[/caption]
បន្ទាប់មកគេប្រើរូបមន្តតង់សង់ (tan) ដើម្បីរកចម្ងាយD ដោយប្រើប្រាស់ដឺក្រេមុំ។ តើគេអាចរកដឺក្រេមុំតែតតាតាមវិធីណា ? ធម្មតាវត្ថុកាន់តែធំហើយឆ្ងាយ នោះអ្នកនឹងមានអារម្មណ៍ថាវាដូចជាគ្មានចលនាផ្លាស់ប្ដូរទីតាំងរបស់វាឡើយ ដូចជាពេលអ្នកជិះម៉ូតូហើយសម្លឹងមើលភ្នំដែលនៅឆ្ងាយដាច់កន្ទុយភ្នែកដូច្នោះដែរ។ ហេតុនេះ គេធៀបទីតាំងរបស់ផ្កាយដែលគេកំពុងរកចម្ងាយនេះ ទៅនឹងផ្កាយដទៃដែលនៅទីឆ្ងាយដែលហាក់ដូចជានៅនឹងថ្កល់មួយកន្លែង នោះគេនឹងអាចរកឃើញមុំតែតតារបស់វាបាន។ ដឹងពីចម្ងាយពីផែនដីទៅព្រះអាទិត្យដែលស្មើនឹង១កាំរបស់១ជុំនៃរង្វិលផែនដី និងដឹងពីមុំរបស់ផ្កាយដែលអ្នកកំពុងរកធៀបនឹងផ្កាយដែលនៅទីឆ្ងាយហើយ គេនឹងអាចគណនារកចម្ងាយD ដែលជាចម្ងាយរបស់ផ្កាយពីផែនដី ដោយប្រើរូបមន្តtanបានហើយ៕
ដោយ៖ ស្រីពៅ
www.space.com[/caption]
Trigonometric Parallex មានពាក្យ Trigonometric ដែលសំដៅទៅលើត្រីកោណមាត្រ និងពាក្យ Parallex ដែលសំដៅទៅលើចំណុចផ្លាស់ប្ដូររបស់ផ្កាយណាមួយដែលគេចង់វាស់ចម្ងាយរបស់វា ធៀបទៅនឹងចំណុចនឹងថ្កល់របស់ផ្កាយដែលមានទីតាំងឆ្ងាយ នៅពេលផែនដីធ្វើចលនាវិលជុំវិញព្រះអាទិត្យដែលជាចំណុចកណ្ដាលរបស់ប្រព័ន្ធព្រះអាទិត្យបានរយៈពេលកន្លះឆ្នាំ។
១ឆ្នាំផែនដីវិលជុំវិញព្រះអាទិត្យបាន១ជុំ ដូច្នេះរយៈពេលកន្លះឆ្នាំផែនដីវិលបានកន្លះជុំ។ ដោយសារចលនារង្វិលជុំរបស់ផែនដីជុំវិញព្រះអាទិត្យមានរាងជាអេលីប នោះផែនដីវិលជុំវិញព្រះអាទិត្យបាន១ជុំ ១ជុំឬ១រង្វង់នេះបង្កើតបានអង្កត់ផ្ចិត។ យើងដឹងថាចម្ងាយពីផែនដីទៅព្រះអាទិត្យមាន១៤៩,៦០០,០០០គីឡូម៉ែត្រ ដែលស្មើនឹងពាក់កណ្ដាលអង្កត់ផ្ចិតរបស់១ជុំឬ១រង្វង់ដែលផែនដីធ្វើចលនាវិលជុំវិញព្រះអាទិត្យបាន១ឆ្នាំ។ ចម្ងាយដែលផែនដីវិលជុំវិញព្រះអាទិត្យបានកន្លះឆ្នាំ ឬជាចម្ងាយពីផែនដីទៅព្រះអាទិត្យតែម្ដងត្រូវបានអ្នកវិទ្យាសាស្ត្រកំណត់យកជាមាត្រដ្ឋានសម្រាប់គណនារកចម្ងាយផ្កាយផ្សេងៗទៀតផងដែរ ដែលគេសរសេរថា ១AU = ៩៣ពាន់លានម៉ៃល៍ (១៤៩,៦០០,០០០គីឡូម៉ែត្រ)។
ដូច្នេះគឺផែនដីជាអ្នកមានចលនារង្វិល ហេតុនេះនៅពេលសម្លឹងមើលផ្កាយ ឧទាហរណ៍ថាក្នុងខែមករា លុះដល់ពេល៦ខែក្រោយមក ឬបានពាក់កណ្ដាលជុំដែលផែនដីវិលជុំវិញព្រះអាទិត្យ នោះអ្នកនឹងសង្កេតឃើញថាផ្កាយដដែលនេះនឹងផ្លាស់ទីទៅម្ខាងទៀត ដែលមានទិសផ្ទុយគ្នានឹងទិសកាលពីអ្នកមើល៦ខែមុន ដូចដែលអ្នកបិទបើកភ្នែកម្ខាងដូច្នោះ។ ចម្ងាយពីផែនដីទៅផ្កាយណាមួយមុននឹងក្រោយ៦ខែ វានឹងជួបគ្នាត្រង់ចំណុចផ្គួបណាមួយ ហើយចម្ងាយពីចំណុចផ្គួបមកកាន់ផែនដីនេះហើយគឺជាចម្ងាយពិតប្រាកដរបស់ផ្កាយនេះពីផែនដី ដែលតាងដែលD។ តើយើងអាចគណនាដូចម្ដេចបាន នៅពេលយើងទទួលបានត្រីកោណនេះហើយ ? ចម្ងាយD នឹងបែងចែកត្រីកោណដ៏ធំមួយនេះជាត្រីកោណកែងពីរ។ អ្នកដឹងហើយថាកំពូលមុំរបស់ត្រីកោណកែងមានរង្វាស់មុំ៩០ដឺក្រេ។
[caption id="attachment_43160" align="aligncenter" width="600"] DrPhysicsA[/caption]
បន្ទាប់មកគេប្រើរូបមន្តតង់សង់ (tan) ដើម្បីរកចម្ងាយD ដោយប្រើប្រាស់ដឺក្រេមុំ។ តើគេអាចរកដឺក្រេមុំតែតតាតាមវិធីណា ? ធម្មតាវត្ថុកាន់តែធំហើយឆ្ងាយ នោះអ្នកនឹងមានអារម្មណ៍ថាវាដូចជាគ្មានចលនាផ្លាស់ប្ដូរទីតាំងរបស់វាឡើយ ដូចជាពេលអ្នកជិះម៉ូតូហើយសម្លឹងមើលភ្នំដែលនៅឆ្ងាយដាច់កន្ទុយភ្នែកដូច្នោះដែរ។ ហេតុនេះ គេធៀបទីតាំងរបស់ផ្កាយដែលគេកំពុងរកចម្ងាយនេះ ទៅនឹងផ្កាយដទៃដែលនៅទីឆ្ងាយដែលហាក់ដូចជានៅនឹងថ្កល់មួយកន្លែង នោះគេនឹងអាចរកឃើញមុំតែតតារបស់វាបាន។ ដឹងពីចម្ងាយពីផែនដីទៅព្រះអាទិត្យដែលស្មើនឹង១កាំរបស់១ជុំនៃរង្វិលផែនដី និងដឹងពីមុំរបស់ផ្កាយដែលអ្នកកំពុងរកធៀបនឹងផ្កាយដែលនៅទីឆ្ងាយហើយ គេនឹងអាចគណនារកចម្ងាយD ដែលជាចម្ងាយរបស់ផ្កាយពីផែនដី ដោយប្រើរូបមន្តtanបានហើយ៕
ដោយ៖ ស្រីពៅ
